Suppose three persons start their journey from position A and finally reach position B [Figure 1]. They did not follow the same path but went through three different paths – ACB, ADB and AEB. ADB is a straight line between them.
In this case, the trajectory of the three must be different, however, since the starting position A and the final position B are the same, it can be said that everyone moved from A to B, meaning that the movement of all three is identical. The minimum distance from A to B is equal to the length of the straight line ADB or AB. This minimum distance is the measure of displacement.

Definition of Displacement: The change of position of a moving object in a particular direction is known as displacement.
Magnitude and direction of displacement:
The magnitude of displacement is the length obtained by adding the first and last position of a moving object. The direction of displacement is from the first position to the last position along that straight line.
Suppose an object travels 3m east from point P to reach point Q and then turns 4m northwards to point R [Figure 2]. The object crossed a total PQ + QR = 7m path. But the displacement of the object is PR. Since PR is the linear distance between the initial position and the final position of the object. Here,
PR2 = PQ2 + QR2 = 32 + 42 = 25
Or, PR = 5m
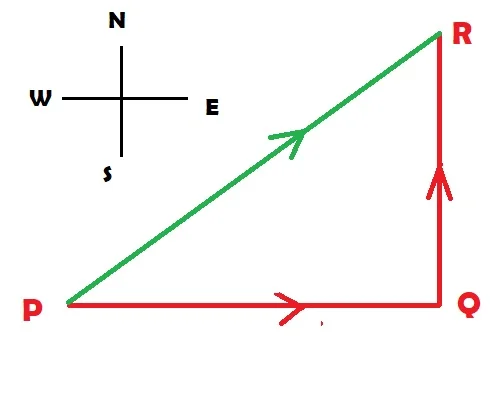
The direction of PR, i.e. the direction from point P to point R is the direction of displacement of the object.
Displacement is a vector quantity:
There are two things in displacement, one is the magnitude and another is the direction. A physical quantity that has magnitude and directions is called a vector quantity. The displacement has both magnitude and direction. So displacement is a vector quantity.
Thus, the displacement does not depend on how an object moved from one position to another. That is, it does not depend on the path, only depends on the initial and final position of the object.
Zero Displacement:
When an object has the same initial and final position, its displacement is zero. That is if a person starts his journey from one place and walks some distance and then returns to that place, then his displacement is zero. After throwing an object vertically from the surface to the up, the object rises slightly and returns to the surface. In this case, the displacement of that object is also zero. So it turns out that even if an object travels some distance, its displacement can be zero. Note that there is no definite direction of zero displacements.
Geometric representation of displacement:
The magnitude and direction of displacement of an object can be determined with the help of a reference frame. Suppose, OX and OY are two axes perpendicular to each other and O is the origin [Figure 3]. An object starts its journey from point O to point A (x, y). Here length OA indicates the magnitude of the displacement of the particle.
|OA| = √ [x2 + y2]
tanθ = AB/OB
or θ = tan-1 (AB/OB)
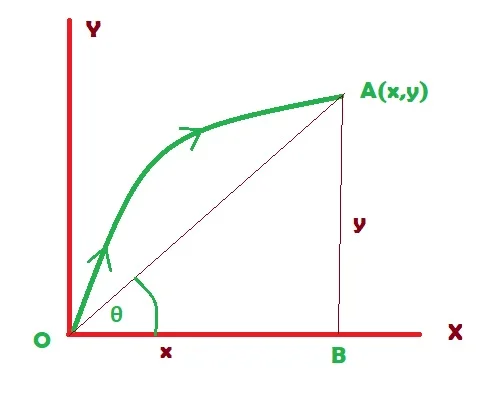
From this we can say, the direction of displacement is along θ = tan-1 (AB/OB), which makes an angle θ with the x-axis.
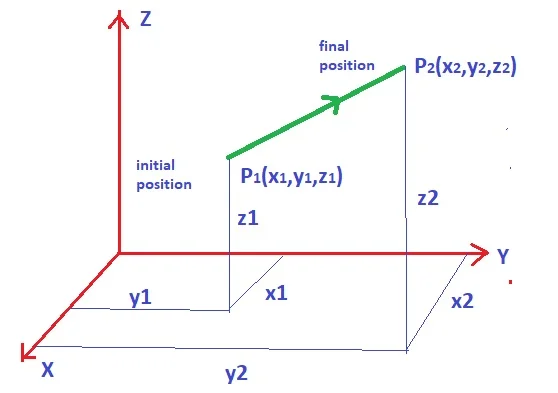
In a cartesian coordinate system, one particle moves from initial position P1( x1,y1,z1 ) to final position P2( x2,y2,z2 ). The magnitude of displacement is given by |P1P2|.
|P1P2| = √ [(x2-x1)2 + (y2-y1) 2 + (z2-z1) 2 ]
Unit and Dimension of Displacement:
The length of a straight line indicates the magnitude of displacement. So the unit of length is the unit of displacement. The different units of displacement are given below.
CGS system: centimeter (cm)
FPS system: feet (ft).
Sl system: Meters (m)
The dimension of displacement is the dimension of length, i.e. [L]
Here is a list of Units: Measurement of Physical Quantity and Unit: Notes
Distance Vs Displacement:
- The term “distance” refers to “how much ground an object has covered” during its travel.
- Displacement is a vector quantity that describes “how far an object is out of place“; it is the object’s overall change in position.
- If a particle moves, the Total distance can be equal to or greater than the displacement.
- If a particle moves, its distance never be zero, but its displacement can be zero if it comes to the same initial point.
Displacement: Problems + Solutions
Problem 1: A particle is moving in a circular path with a radius 7 cm. (I) What is the displacement when the particle moves half of its circular path? (ii) What is the displacement when the particle completes one circular path?

Solution:
(I) The circumference of the circle is 2𝝅r = 2 . (22/7) . 7 = 44 cm.
Distance covered in this case (point A to point B i.e AB) is 44/2 = 22 cm.
So the displacement AB is 22 cm and its direction is from point A to point B.
(ii) When the particle completes the circular path, it travels a path equal to the length of the circumference. So the path passed = 44 cm. In this case, since the particle returns to its initial position after the start of the journey, the displacement = 0.
Problem-2: An object moves 10 √ 3 m along the east. After that, it turns north and moves 10 m. What would be the magnitude and direction of displacement?
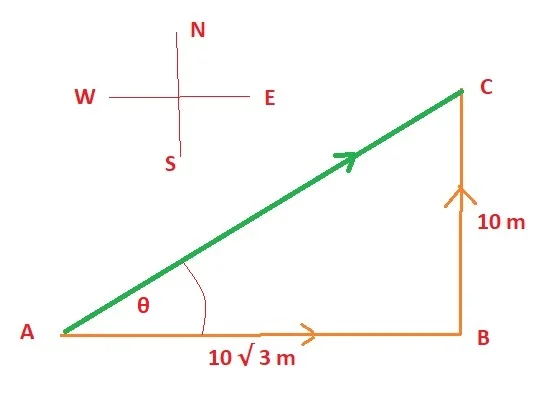
Solution:
Here AB = 10√3 m , BC = 10m. As the initial position of the particle is A and the final position is C, the displacement is AC.
AC = √ (AB2=BC2)
= √ [(10√ 3)2 = (10)2]
= √ [300+100]
= 20 m
Now, if the displacement AC makes an angle θ with AB, then,
tan θ = BC/AB
= 10/(10√3)
= 1/ √3
= tan 30°
Therefore θ = 30°. This angle gives us the direction of displacement.
Important Points for Competitive Govt Job exams:
- Displacement is the shortest distance between two points that has a direction from the initial to the final point.
- Displacement is a vector quantity.
- SI and cgs unit of displacement is meter and centimeter respectively.
- The dimension of displacement is [L].
