Speed
Definition of Speed: The rate of change of distance with respect to time is called speed.
Alternate Definition: The distance covered by an object per unit time is called speed.
Distance is always measured along the path passed by an object. That is, to measure the distance, one has to determine the length of the path as long as it travels in a straight or curved path. Thus, any object when it travels a distance in a time t, then-
$$speed\:(s) = \frac{ distance \: (l)}{time\: (t)}$$
Speed is a scalar quantity:
There is no definite direction of distance or path traveled by an object (in the case of speed). For example, a train has traveled 50km in 2 hours (i.e. speed is 25 km/h) – this statement does not indicate any specific direction of motion. In general, the movement of the train is sometimes straight, sometimes crooked. So there is no specific direction of speed. A physical quantity that has only magnitude but no definite direction is called a scalar quantity. Thus, speed is a scalar quantity.
Unit of Speed
As we know speed = distance/time, so
Unit of speed = unit of distance/ unit of time
i.e. unit of speed = meter/second in the SI system.
SI System: The unit of speed is- m/s
CGS System: The unit of speed is – cm/s
FPS System: The unit of speed is – ft/s
1 km/h = 1000m/3600s = (5/18)m/s.
What is the Dimension of Speed?
Dimension of Speed = dimension of distance/dimension of time
Thus Dimension of speed = [L]/[T] = [LT-1]
Uniform Speed: If an object covers an equal distance in equal intervals of time, then its speed is called uniform speed.
Average Speed:
If an object travels a different distance in an equal interval of time, then its speed is called variable speed. For variable speed, we can calculate the average speed. Let us assume, an object travels l1 distance in t1 time, l2 distance in t2 time, and l3 distance in t3 time. Therefore the total distance is (l1+l2+l3 ) and the total time is (t1+t2+t3). Thus
Average Speed = Total distance/total time
Instantaneous Speed:
If an object has a uniform speed then in any instance the instantaneous speed is equal to its uniform speed.
Velocity:
Definition of Velocity: The rate of change of displacement with respect to time is called velocity.
Alternate Definition: The amount of displacement per unit time is known as velocity.
Read here about Displacement: Displacement: Concept Example Problem Solution
Velocity is a vector quantity: We know that displacement is a vector quantity i.e. it has a magnitude and definite direction. Therefore velocity is also a vector quantity. Velocity also has a magnitude and direction.
Unit of Velocity:
Unit of velocity = unit of displacement/unit of time
SI unit of velocity = m/s
CGS unit of velocity = cm/s
FPS unit of velocity = ft/s
Dimension of Velocity:
Dimension of velocity = dimension of displacement/dimension of time
Uniform Velocity: If an object moves an equal amount of displacement in an equal interval of time, then we can say that it has uniform velocity.
Average Velocity: Average velocity is calculated by the change of total displacement (s) divided by total time (t).
Average Velocity <v>
Instanteneous velocity =
Uniform Velocity: If the magnitude of velocity and direction both remain the same in all instances then its velocity is uniform.
Non-uniform Velocity: If the magnitude of velocity or the direction or both changes with respect to time, then its velocity is non-uniform.
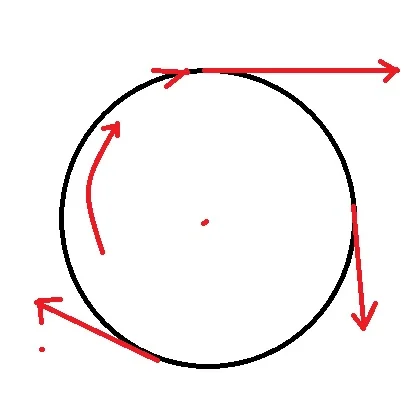
Circular Motion: If an object revolves around a circular path and it covers an equal amount of path in equal time, then we can say that its speed is uniform. But in this case, we can not say that its velocity remains the same in all instances. Because the direction of velocity is always changing. From the figure below we can easily see that the red direction is changing at all positions.
Speed Vs Velocity: Comparison
| No | Speed | Velocity |
|---|---|---|
| 1. | Speed = Distance/time | Velocity = Displacement/time |
| 2. | Speed is a scalar quantity; it has only a magnitude | Velocity is a vector quantity; it has both magnitude and direction. |
| 3. | Speed can not be negative, because the covered distance never be negative. | Velocity can be negative; because if we take positive along the east it will be negative along the west. |
| 4. | If the average speed is zero then its average velocity must not be zero. | If the average velocity is zero then its average speed may not be zero. |
Speed Velocity: Problem + Solution
Problem-1: If An object is moving around a circular path of radius 7 cm. After time t=5 seconds it moves half of its circular path and t=8 seconds, it travels a complete circular path. Find the speed and velocity in both cases.
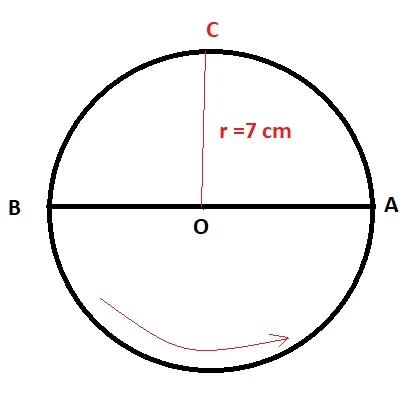
Solution:
The total path for one complete revolution = circumference of the circle = 2πr; where r is the radius of the circle
= 2 × (22/7) × 7 = 44 cm
Case 1: When the object travels half of the circular path. The total distance = (44/2) = 22 cm.
Speed = 22/5 = 4.4 cm/s
Here displacement = AB path along A to B = 14 cm
$$velocity \overrightarrow{v} = \frac{\overrightarrow{AB}}{t}$$
$$= 14/5 = 2.8 cm/s \:along \:A \:to\: B$$
Case 2: In this case total path = circumference of circle = 2πr = 44 cm
Speed = 44/8 = 5.5 cm/s
Total displacement = 0. Because for one complete revolution object comes to its original position I,e the initial and final positions are the same.
Velocity = 0/8 = 0 cm/s
Problem-2: A train starts moving from station A to B at 40 km/h. After that, it comes to A from B at 60 km/h. Calculate the speed and velocity of the train.
Answer:
Solution:
Let us consider the distance between the two stations A and B is = x km.
So it takes time to go from station A to B is = x/40 h.
Again it also takes time to come back from station B to A is = x/60 h.
Now
$$average\: speed = \frac{total \: distance}{total\:time}$$
$$ = 48 \:km/h$$
As the initial and final position of the train is the same I,e. the train starts moving from station A to B and comes again to station B, its total displacement is = 0;
$$average\:velocity = \frac{total\:displacement}{total\:time}$$
$$= \frac{0}{total\:time} = 0$$
Problem-3: Let us consider an object that moves along the x-axis. It follows this equation of motion:
x= 7t+5t2
- find the average velocity between time t= 0 to t= 2 seconds.
- find the instantaneous velocity at time t=3 seconds.
Answer:
Solution:
(1) Here x= 7t+5t2
when t = 0s; displacement x = x1 = 7× 0+5×0 = 0 m;
when t=2s; x2 = 7×2+5×22 = 34 m;
Therefore displacement = x2 – x1 = 34 – 0 = 34 m;
total time t = 2 – 0 = 2 s.
Average velocity = 34/2 = 17 m/s;
Here x= 7t+5t2
$$\overrightarrow{v} = \frac{\mathrm{d} }{\mathrm{d} t} (7t+5t^{2})$$
$$ = \: (7+10t)$$
$$t=3s; v= 7+ 10×3 $$
$$ = 37 \:m/s $$
Summary: Speed & Velocity: Important GK
- Speed is the rate of change of distance per unit of time.
- Speed is a scalar quantity
- SI and CGS units of speed are m/s and cm/s respectively.
- Dimension of speed is [LT-1]
- Velocity is the rate of change of displacement per unit time
- Velocity is a vector quantity.
- Units of velocity and speed are the same. SI and CGS units of velocity are m/s and cm/s respectively.
- Dimension of velocity and speed is same i,e [LT-1].
- Speed can be greater than or equal to |vilocity|. || indicates the magnitude.
Practice Problems from Speed and Velocity:
Exercise-1. An object covers a distance half of the circle along its circumference in a time of 3 s. If the radius of the circle is 9m, then calculate the velocity of the object. [Ans: 6m/s].
Exercise-2: A person goes a certain distance. He goes half of the distance with 30 km/h and the rest half with 40 km/h. What is his average speed? [Ans: 34.3 km/h]
Exercise-3: How much distance can travel by an object in 1 second if its speed is 18km/h? [Ans: 5m]
Exercise-4: A bike went first 1/3 of its total distance with a speed of 10 km/h, the second 1/3 goes with 20 km/h, and the rest 1/3 goes with 60 km/h. Calculate its average speed. [Ans: 18 km/h]
Exercise-5: A 500m long train completely passes a bridge of 1000m in 10 s. Calculate its Velocity. [Ans: 150 m/s]
