Angular Displacement
Definition: The angle formed by the center of the initial and final position of a rotating particle is called the angular displacement.
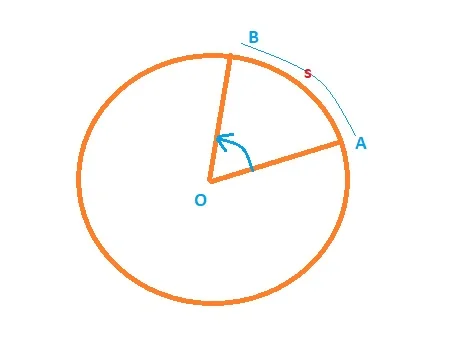
Suppose a particle has an initial position at point A whose angular coordinate is θ1 and its final position is at point B whose angular coordinate is θ2 [Figure 1]. Thus the magnitude of angular displacement of the particle, to move from point A to B, i.e. to the path AB, is ∠AOB = θ2 – θ1.
Angular displacement is scalar or vector? The Answer
As of now, we are able to know how to measure the magnitude of angular displacement. Is angular displacement a vector quantity? If the answer is yes, then what is the direction of angular displacement? We already know that linear displacement has a real particular direction, then what about angular displacement? So to find the answer we need to know a few things.-
Measurement of Angles:
A common unit of measurement of angles is the degree. Also, when drawing a circle centering on the vertex of an angle, the angle is measured by the ratio of the length of the circular path (i.e arc) in front of that angle to the radius of the circle.
θ = ∠AOB = Arc Length / Radius
Thus the unit of angle is obtained as radian (or rad for short).
Definition of 1°: The angle at which the arc of a circle of length equal to the radius of a circle forms the center of that circle is called 1 radian.
However, the common unit of angle is also degree (°).
1° = (π/180) rad
or 1 rad = 57.296°
The angle is a dimensionless quantity because it is the ratio of two lengths. Thus angular displacement is a dimensionless physical quantity when it is measured in radians.
Polar Vector:
We know that linear displacement, velocity, and acceleration are vector quantities. These vectors have a real particular direction. These are called polar vectors.
Axial Vector:
Similarly, angular displacement, angular velocity, and angular acceleration are also vector quantities because they also need a particular direction to completely specify them. We may assume that this particular direction is along the axis of rotation.
A particle can move clockwise or anticlockwise in a circular path. Clockwise and anticlockwise motions are opposite to each other. So, how to find the direction of axial-vector or angular displacement? The common practice is that if the direction of rotation of a (right-handed) screw is the direction of rotation of a particle (i.e. anticlockwise), then the direction of progress of the screw is the direction of the axial vector or the angular displacement. For example, when a dew on a table is opened with a lid patch, the lid rotates counterclockwise (when viewed from above) and the lid moves upwards. Also, this can be determined using the right-hand thumb rule. Learn more about the Right-hand Rule here.
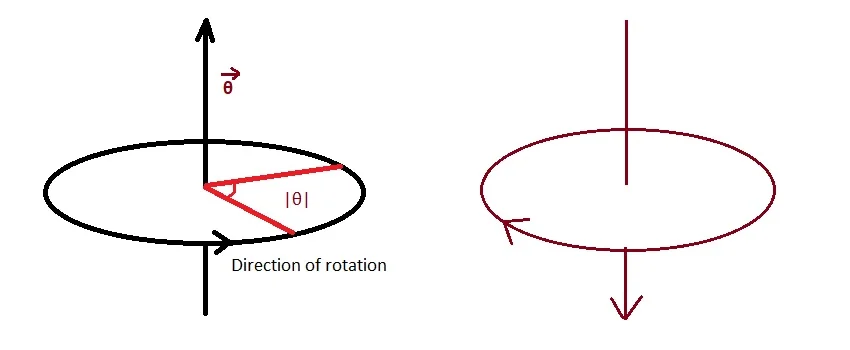

Therefore after understanding the axial vector, we easily conclude that angular displacement is a vector quantity.
! Alert: Angular displacement is not really a vector since it does not obey the commutative law of addition while possessing direction and magnitude. You will learn more about it when you learn the Tensor quantity.
Relation Between Linear and Angular Displacement:
We know that, θ = Arc Length / Radius = s/r
or, s = r × θ. (formula of angular displacement.)
So, Distance = radius × angular displacement.
But wait, here “s” is not really linear displacement, it is not just a straight line. “s” just measures the distance (s) as a scalar quantity, and the direction of “s” continuously changes.