Angular Velocity: Definition Unit Formula Concept

Q: What is the unit of angular velocity?

The cgs and SI unit of angular velocity is <strong>rad/second</strong>.

Angular Velocity: Theory & Concept

Definition of Angular Velocity: The rate of change of angular displacement with respect to time is called angular velocity. It is also defined as the change of angular displacement per unit of time.

Table of contents

That is, the angle that a particle moving in a circular path produces at the center of rotation at a unit time is called the angular velocity of the particle. If a particle moves in a uniform circular motion and makes an angle θ at time t then –

$$angular\:velocity \:(\overrightarrow{\omega})= \frac{angular\:displacement\overrightarrow{\:(\theta)}}{time(t)}$$

$$\overrightarrow{\omega}= \frac{\overrightarrow{\:\theta}}{t}$$

Instantaneous Angular Velocity:

The angular displacement (Δθ) of a particle located at a point in a very short time (Δt) is called instantaneous angular velocity. Mathematically it is defined as, –

$$\overrightarrow{\omega } = \displaystyle \lim_{\Delta t \to 0}\frac{\Delta\overrightarrow{\theta } }{\Delta t} = \frac{d\overrightarrow{\theta }}{dt}$$

Is angular velocity a vector?

As we know that angular displacement is an axial vector, the angular velocity is also an axial vector. Therefore the angular velocity is a vector quantity. Its direction is along the axis of rotation following the right-hand rule.

Attention!! Angular velocity is actually a pseudovector (defined as a function of some vectors).

The Right-Hand Thumb Rule:

The right-hand thumb rule is used to determine the direction of angular velocity. For a better idea, let us consider a disk rotating counterclockwise (figure-1). Also, we shall consider the axis of rotation as a pole passing through the center of the disc. Using the right-hand rule, we would hold the pole with our right hand so that our four fingers follow the rotational direction. In addition, our thumb is perpendicular to our other fingers, pointing straight out on the axis.

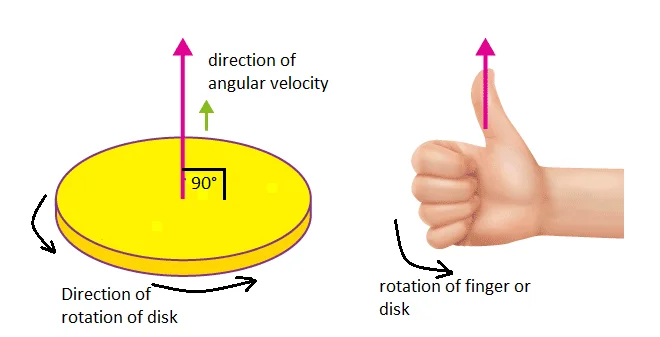
Think About: What is the direction of the minute hand of a wall clock?

Unit and Dimension of angular velocity:

We know that the unit of angular displacement is – radian. Therefore, the unit of angular velocity is radian/second.

The dimension can be obtained as follows.

Angular velocity = (angular displacement) / time
Dimension of angular velocity = (dimension of angular displacement)/ dimension of time
Dimension of angular velocity = 1/[T] = [T^–1]

Time Period: The time taken by a body to complete one rotation is known as the time period. It is denoted by T. Its unit is second both in cgs and SI system, and its dimension is [T]. To complete one rotation by a body, it takes time T and its angular displacement is θ = 2π, then

$$\omega = \frac{2\pi}{T}\: or \: T = \frac{2\pi}{\omega } $$

Angular Frequency: The angular frequency is defined as the number of complete rotations (complete oscillation or complete revolution) per unit of time (i.e. in 1 second). The frequency denotes the rotation speed or the magnitude of angular velocity. It is also known as the angular frequency vector which vector measures the rotation rate.

Relation between Angular frequency and linear frequency:

The frequency f means a particle complete f-number of rotations in one second.
For one complete rotation, the angular displacement is = 2π
For f-number of complete rotation, the angular displacement is = 2πf
ω = angular displacement/time
So, ω = 2πf / (1 sec)
ω = 2πf [This is the relation between linear and angular frequency]

$$f = \frac{\omega }{2\pi} $$

Now putting the value ω = 2π/T in the above equation we get

$$f = \frac{\omega }{2\pi}\: = (\frac{2\pi}{T})\times \frac{1}{2\pi}$$

$$f = \frac{1}{T}$$

1 rpm equals π/30 (about 0.105) rad/second.

Relation between Linear and Angular Velocity:

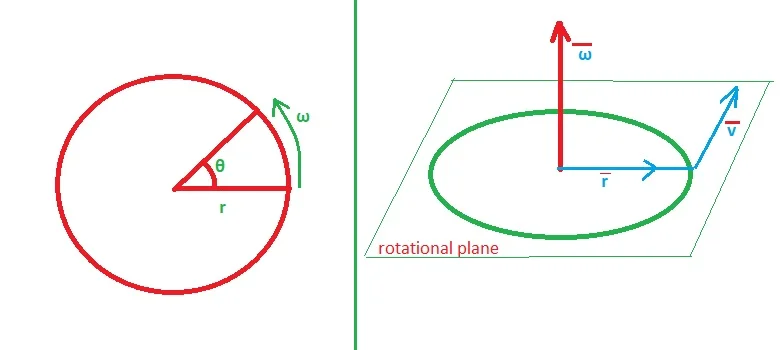
Now let us consider the angular velocity of a particle is = ω
It rotates about a circular path of radius = r
After time t it covers an arc length = s
Also, after time t its angular displacement is = θ
According to definition ω = θ/t
Now, if the linear speed of the particle is = v, then

$$v = \frac{s}{t}\: = \frac{r\theta }{t}\:= \omega r$$

Therefore, Speed = angular velocity × radius

In this case, the magnitude of linear velocity and speed is the same so that the magnitude of linear velocity = angular velocity × radius.

The vector form of the above formula is –

$$\overrightarrow{v}=\overrightarrow{\omega}\times \overrightarrow{r}$$

Angular Velocity: Exercise Practice

Exercise-1: Find the angular velocity of the second hand, minute hand, and hour hand of a wall clock. Also, point out the direction.

We know that the second hand completely rotates around the clock in 60 seconds, i.e. it covers a total angular displacement of 2π in 60 seconds. So the angular velocity of the second hand is –

$$\omega = \frac{2\pi}{60}\:= 0.105\: rad/sec$$

The minute hand covers a total of 2π angle in 60 minutes = 3600 seconds. So, the angular velocity of the minute hand is

$$\omega = \frac{2\pi}{3060}\:= 1.075\: \times 10^{-3}\: rad/sec$$

Similarly, the hour hand covers a total of 2π angle in 12 hours = 21600 seconds. The angular velocity of the hour hand is

$$\omega = \frac{2\pi}{21600}\:= 1.45\: \times 10^{-4}\: rad/sec$$

The direction of each hand is the same, which is outward from the wall or the surface of the wall clock.

Attention: The angular velocity ω = 2π/t. π is a unitless quantity. So the unit of ω is /second. However, we put the unit of pi as rad so that the unit of ω becomes rad/sec.

Exercise-2: A car rotates around a circular path of a radius of 20 m at a velocity of 40 km/h. What is the angular velocity of this car?

Answer: The linear velocity of the car v = 40 km/h = 100/9 (m/s). Therefore, the angular velocity of the car would be –

$$\omega = \frac{v}{r} = \frac{100}{9\times 20} = \frac{5}{9} = 0.56\: rad/sec$$

Exercise-3: When the minute hand and hour hand of a clock will meet each other?

Let us consider the two hands meet each other after time t. For hour hand ω = 2π/12 = π/6 rad/hour. Therefore the angular displacement of hour hand after time t is θ = ωt = πt/6 rad.

On the other hand, the angular velocity of the minute hand is ω’ = 2π/1 rad/hour. And the angular displacement of the minute hand is θ’ = ω’t = 2πt/1 rad.

The two hands meet again after time t hours. The minute hand covers one extra rotation i.e 2π angle after t hour.

So, θ’ – θ = 2π
or, 2πt – πt/6 = 2π
or, t = 12/11 hour = 1 hour 5 minutes and 27 seconds.

Exercise-4: What is the angular velocity of the Earth rotation?

The earth rotates around its axis in 24 hours = 864000 seconds. So the angular displacement is 2π

$$\omega = \frac{2\pi}{864000}\:= 7.3\: \times 10^{-5}\: rad/sec$$

Angular Velocity: Question Answers

What is angular velocity?

Angular velocity is the time rate of change of angular displacement.

What is the unit of angular velocity?

The cgs and SI unit of angular velocity is rad/second.

Does angular velocity have a direction?

Yes! Angular velocity has a particular direction following the right-hand thumb rule. Its direction is along the axis of rotation, i.e. perpendicular to the plane of rotation. Actually, it is a vector quantity because angular displacement is a vector quantity.

Is angular velocity the same for the different radii of the same centered circle?

The angular velocity for the same centered circle at the different points is the same. However, the tangential velocity or linear velocity has different magnitude for different points. Actually the tangential velocity increase as increase the radius.

Suggested Readings:

Angular Displacement	Speed & Velocity
Displacement: Concept	Measurement of Physical Quantity and Unit

Angular Velocity Study Notes

Download PDF