Definition: A particle orbiting in a circular path with uniform speed always has an acceleration towards the center of the circle which is called radial acceleration or normal acceleration or centripetal acceleration.
If a particle has an angular velocity ω rotates in a circular path of radius r, then its centripetal acceleration is
ac = ω2r = v2/r
Note that the velocity of the particle is always along the tangent to the circle, but the centripetal acceleration is always towards the center of that circle. Thus, in a uniform circular motion, the velocity and centripetal acceleration are perpendicular to each other.
Derivation of Centripetal Acceleration
When an object moves around a circular path, its direction constantly changes, and thus its linear velocity does not remain the same. This changing velocity in a circular motion produces an acceleration that is always directed to the center of the circle. This is known as centripetal acceleration. Here, mathematically we will deduce the formula of centripetal acceleration in a simple way.
Let us consider a particle of mass m rotating around a circular path of radius r with uniform linear velocity v. For a very short time t (t → 0) the particle moves from point A to point B. As a result, it makes an angle θ (= ∠AOB) at the center of the circle. So, the angular velocity of the particle is ω = θ/t.
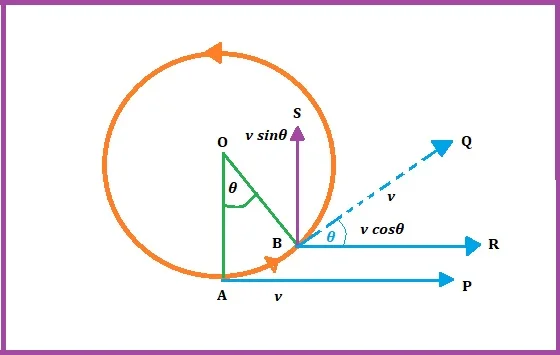
At point A, the linear velocity of the particle is v along the tangent AP. The component of this velocity along the radius AO is zero because AO and AP are mutually perpendicular.
At point B, the velocity of the particle is v along with BQ. At this point, v can be divided into two perpendicular components. One is v.cosθ parallel to Ap and along with BR, and the other is v.sinθ parallel to AO and along with the direction BS.
If θ is very small such that θ → 0, then we may consider sinθ = θ and cosθ = 1. Again if the angle ∠AOB is very small then BR and BS also can be considered to overlap on AP and AO respectively.
So along AB, the initial velocity of the particle is = v, and the final velocity is vcosθ = v. This means the change in velocity is (v − v) = 0
or, acceleration at = change in veolcity/time = 0/t = 0.
That is along the direction AP or along the tangent of the circle, the acceleration of the particle is zero.
Now, along the direction AO, the particle’s initial velocity is = 0, and the final velocity = vsinθ = vθ.
or, change in velocity = (vθ − 0) = vθ.
or, acceleration along AP is ac = vθ/t
or, ac = vω [as ω = θ/t]
or, ac = (ωr)r
or, ac = ω2r = (v/r)2r = v2/r.
Thus there exists an acceleration along the center of the circle. This acceleration is called centripetal acceleration.
Therefore the formula of centripetal acceleration is:
- Where ac = centripetal acceleration
- v = linear velocity
- r = radius of the circle
- ω = angular velocity.
Think About it: Can a particle have acceleration while moving with constant speed?
Centripetal Acceleration: Unit and Dimension
Unit of centripetal acceleration = (unit of velocity)2 / (unit of radius)
= (m/s)2 / m
= m/s2
Dimension of centripetal acceleration = [dimension of velocity]2 / [dimension of radius)]
= [LT−1]2 / [L]
= [LT−2]
| SI unit of centripetal acceleration | m/s2 |
| CGS unit of centripetal acceleration | cm/s2 |
| FPS unit of centripetal acceleration | ft/s2 |
| Dimension of centripetal acceleration | [LT−2] |
Centripetal Acceleration: Vector Form:
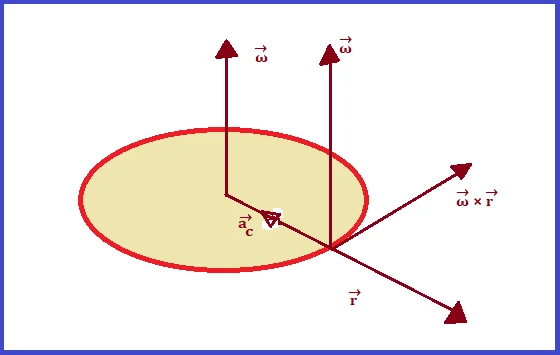
Centripetal acceleration is a vector quantity. It has both magnitude and direction. Its direction is always toward the center of the circle.
The relation between the linear and angular velocity in vector form is given by –
Differentiating with respect to time t we get-
$$\frac{d\overrightarrow{v}}{dt} = \omega \times \frac{d\overrightarrow{r}}{dt} + \overrightarrow{r} \times \frac{d\overrightarrow{\omega} }{dt}$$
$$or, \overrightarrow{a} = \overrightarrow{\omega} \times \overrightarrow{v} + \overrightarrow{r} \times \overrightarrow{\alpha} $$
$$or, \overrightarrow{a} = \overrightarrow{a_{c}}+\overrightarrow{a_{t}}$$
Where α is the angular acceleration. Thus we can see that when an object rotates around a circular path consists of two kinds of accelerations, ac and at. ac is called the centripetal acceleration which is always directed toward the center of the circle and at is the tangential component. Both are perpendicular to each other. The net or resultant acceleration is-
Note that-
$$\overrightarrow{a_{c}} = \overrightarrow{\omega} \times \overrightarrow{v} $$
$$or, \overrightarrow{a_{c}} = \overrightarrow{\omega} \times (\overrightarrow{\omega} \times \overrightarrow{r})$$
– which is the vector form of centripetal acceleration.
Think About: Which physical quantity remains the same in a uniform circular motion?
Centripetal Acceleration: Problem Solutions
A person is rotating a rod of length 10m. Calculate the angular velocity needed to generate centripetal acceleration 5 times gravitational acceleration.
Answer:
Here in this problem, the given data are – r = 10m,
centripetal acceleration ac = 5g, where g = 10 m/s2 = gravitational acceleration.
We know, ac = ω2r
or, ω2 = ac / r = 3g / r
or ω2 = (5 × 10) / 10
or, ω2 = 5
or, ω = √5
∴ ω = 2.236 rad/sec
Thus the required angular velocity is 2.236 rad/sec.
Find the radial acceleration of an hour hand of a wall clock having a length of 0.2 m.
Answer:
For the hour hand, the time period T = 12 hours, and r = 0.2 m.
So its angular velocity ω = 2π / T = 2π/12 = 2π / (12×3600) = 1.454 × 10−4 rad/sec.
Its linear velocity v = ωr = 1.454 × 10−4 × 0.2 = 2.9 × 10−5 m/s
Its radial acceleration ac = v2/r = (2.9 × 10−5)2 / 0.2
∴ ac = 4.228 × 10−9 m/s2
Thus the radial acceleration of an hour hand of 0.2 m is 4.228 × 10−9 m/s2.
Few Questions Answers
Look Back at Your Knowledge
Which is the correct formula for centripetal acceleration?
v2/r
v/r
v2r
vr
[v2/r]
A long bar of length 2m is rotating around the center with an angular velocity of 2 rad/s. What would be the radial acceleration?
3 m/s2
4 m/s2
5 m/s2
6 m/s2
[4 m/s2]
A ball of radius 4 cm rotating with a uniform speed of 4 cm/s. what is its radial acceleration?
4 cm/s2
16 cm/s2
64 cm/s2
2 cm/s2
[4 cm/s2]
Which is not the correct formula of centripetal acceleration?
v2/r
ω2r
ωv
ωr
[ωr]
Suggested Readings:
Centripetal Acceleration Notes
