Definition of Angular Momentum: The moment of inertia and angular velocity relative to an axis which together creates a dynamic property of a rotating object is called the angular momentum of the object relative to that axis.
Angular momentum is the rotational analog of linear momentum. It is an important physical quantity in physics.
Table of contents
- Angular Momentum: A scalar or Vector?
- Unit and Dimension of Angular Momentum:
- Relation between Linear and Angular Momentum:
- Relation Between Angular Momentum and Torque:
- Law of conservation of Angular Momentum:
- What is the physical significance of angular momentum?
- Angular Momentum: Question Answers
- Look Back at your Knowledge
Mathematically, the magnitude of angular momentum (L) is the product of the moment of inertia (I) and angular velocity (ω).
Formula of Angular Momentum: L = Iω
- Where L = angular momentum
- I = Moment of Inertia;
- ω = Angular Momentum.
Angular Momentum: A scalar or Vector?
As the angular velocity is an axial vector, the angular momentum is also an axial vector. This means, the angular momentum is a vector quantity – it has both the magnitude and the direction. Its direction follows the right-hand thumb rule. If a particle rotates anticlockwise, the direction of angular momentum is perpendicular (outward) to the plane of rotation.
Think About: What is the direction of angular momentum of the ceiling fan?
Unit and Dimension of Angular Momentum:
Angular momentum = [moment of inertia] × [Angular velocity]
Unit of Angular momentum = [unit of moment of inertia] × [unit of Angular velocity]
Unit of Angular Momentum = [kg-m2] /[sec]
Therefore the unit of Angular momentum is kg-m2/sec
Note: In the unit of angular velocity (radian/second), we removed the radian. Because it is a dimensionless quantity.
Dimension of Angular Momentum:
[Dimension of Angular momentum] = [Dimension of moment of inertia] × [Dimension of Angular velocity]
[Dimension of Angular momentum] = [ML2] × [T –1]
[Dimension of Angular momentum] = [ML2T−1]
Relation between Linear and Angular Momentum:
Let us consider a body is rotating with angular velocity ω about an axis. The body can be considered as a large number of particles with masses of m1, m2, m3, … .etc. which are located at distances r1, r2, r3, …. .etc. respectively. So the moment of inertia I = (m1r12 + m2r22 + m3r32 + ….). or,
For pure rotation, all the particles consist of the same angular velocity.
Also, we know that the linear momentum p = mass × linear velocity.
So the angular momentum L = rotational equivalent of mass × angular velocity.
or, L = I × ω
L = Σmr2ω = Σmvr
Where v = ωr
For each particle, the terms r1 × m1v1, r2 × m2v2, … are can be called the moment of linear momentum or moment of momentum. Here, if ω = 1, the angular momentum L = I. So the moment of inertia of a body about the axis is numerically equal to the moment of momentum of the body rotating with unit angular velocity.
Thus the angular momentum is the algebraic sum of the moments of momentum of all the particles.
Now, if a particle rotates around an axis of radius r with linear velocity v, (so that its linear momentum p = mv) then, the angular momentum L = r × p.
Vector Form of Angular Momentum: The vector relation between linear and angular momentum is
If the linear momentum vector and the radius vector make an angle θ, then:
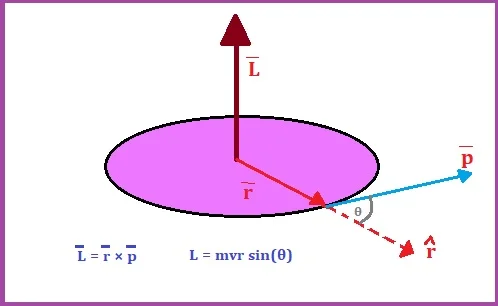
Extra Info: For the motion of a particle under a central force field, the angular momentum vector remains constant, and the orbit of the particle is such that for any value of r and dr/dt on it, there is a constant vector associated, and hence the orbit described will lie is a plane.
Relation Between Angular Momentum and Torque:
For rotational motion, the angular acceleration is produced by the application of Torque.
Let the initial angular velocity of a particle is = ω1. After time t, its final angular velocity is ω2.
So, the angular acceleration of the particle is = α = (ω2 − ω1)/t.
Again Torque = moment of inertia × angular acceleration
or, τ = I × α
or, τ = I × (ω2 − ω1)/t = (Iω2 − Iω1)/t
or τt = (Iω2 − Iω1) = ΔL = change in angular momentum.
Torque × time = Change in angular momentum.
Here the term τ × t is called angular impulse.
In differential form:
Think About: To find an angular impulse, what do we multiply by a change in time?
Law of conservation of Angular Momentum:
When the external torque τ = 0, i,e. when there is no external torque on an object, form the equation τt = (Iω2 − Iω1) we get (Iω2 − Iω1) = 0.
or Iω2 = Iω1.
This means that if there is no external torque applied to the particle, the initial momentum of a particle is equal to the final momentum, or simply for non-relativistic cases where the mass is constant, the initial angular velocity remains the same as the final angular velocity.
Statement: The angular momentum of a particle with respect to an axis is remain the same (conserved) when there is no external torque applied to the particle.
Clearly, the law of conservation of angular momentum in rotational motion is a replica or equivalent to the law of conservation of linear momentum in linear motion.
Here from the equation: τ = dL/dt, we can say that, if the external torque τ = 0, the term dL/dt becomes zero. Therefore, L = constant.
Think About: Which is the correct formula for Newton’s 2nd law in rotational motion?
Practical examples of Angular Momentum:
A man is sitting on a rolling table with two dumbbells of equal weight in his arms, and the table rotates at a certain angular speed. When the man brought the two dumbbells close to his body, it was seen that the table started rotating faster. This is because the moment of inertia of the man relative to the axis of rotation decreases when the two hands are brought close together; As the angular momentum is preserved, its angular velocity increases. Then, when the arms are stretched again, the moment of inertia of the man increases with respect to the axis of rotation. Thus, its angular velocity decreases and the table rotates slowly.
When a competitor in a diving event jumps into the water from a high platform, he jumps with his arms and legs as wide as possible at the beginning, that is, he falls with a small amount of angular velocity. Then whenever he folds his arms and legs, his moment of inertia decreases, and his angular velocity increases. As the angular momentum is preserved, the angular velocity increases i.e. the body rotates very fast. That’s why he can achieve more than one somersault before falling into the water. Angular momentum conservation formulas are similarly used when skating on ice or performing acrobatic games.
Also, the second law of Kepler for planetary motion is a direct consequence of the law of conservation of angular momentum in classical mechanics.
What is the physical significance of angular momentum?
- Linear momentum is used to describe the ” magnitude” of linear motion. In some ways, this means that linear momentum tells us how much impulse is needed to stop an object in linear motion.
- Now, whatever the meaning of linear momentum is in linear motion, angular momentum has the same meaning in a rotating motion. It shows us how much angular impulse will be necessary to stop the object in rotating motion.
- The law of conservation of angular momentum is analogous to the law of conservation of linear momentum. Both linear and angular momenta are treated as observables in quantum mechanics, with associated operators.
Exercise-1: If the radius of the earth decreases about 1/2%, then what will be the length of a day? mass of the earth is constant.
We know that the formula of the moment of inertia is I = mr2. If the mass of the earth remains the same, then
I ∝ r2 where r is the radius of the earth.
In this case, after reducing, the radius of the earth r’ = (100 − 0.5)r/100 = 199r/200.
Now after reducing the radius of the earth, the final moment of inertia is I’.
= (200/199)2
Let the length of a day is T before and T’ after reducing its radius. If the initial and final angular velocity of the earth is ω and ω’, then, according to the law of conservation of angular momentum
Iω = Iω’
or ω’ = (I/I’)ω
or, 2π/T’ = (I/I’) × (2π/T)
or, T’ = (I/I’)×T
or, T’ = (199/200)2 × 24
∴ T = 23.76 hours
∴ The length of the day will be reduced is (24 – 32.76) = 14 min 24 sec.
Exercise-2: A person is pushing a wheel by applying torque 20 N-m. The wheel has a moment of inertia of 50 kg.m2. What will be its rotational speed after 5 seconds assuming it starts at rest?
The angular momentum L = τ × t = 20 × 5 = 100 kg⋅m2/s.
Also, the formula of angular momentum is L = Iω.
L = Iω
or, 100 = 50ω
or, ω = 100/50
∴ ω = 2 /sec.
Exercise-3: If the moment of inertia of a rotating object is halved then what will be the angular velocity of the object?
The formula of angular momentum is L = Iω.
Let the initial moment of inertial is I1.
Initial angular velocity = ω1.
The final moment of inertial is I2 = I1/2.
and the final angular velocity = ω2.
If the initial and final angular momentum is L1 and L2 respectively, then according to the conservation of angular momentum:
L1 = L2
or, I1ω1 = I2ω2
or, I1ω1 = ( I1/2) × ω2
or, ω2 = 2 ω1
∴ So, the final angular velocity would be double its initial value.
Problem-1: If the radius of the earth increases double its initial value, then how many hours will be a day?
Problem-2: If the moment of inertia of a disc is double then what will be the angular velocity of the disc?
Angular Momentum: Question Answers
Angular Momentum: Study Notes
Look Back at your Knowledge
Angular momentum =
| [A] moment of Inertia × angular velocity |
| [B] moment of inertia × torque |
| [C] torque × angular velocity |
| [D] torque × angular acceleration |
Answer:
[moment of Inertia × angular velocity]
The formula of angular momentum is
| [A] mv/r |
| [B] mvr |
| [C] mr/v |
| [D] rv/m |
Answer:
[mvr]
Unit of angular momentum is
| [A] kg-m/second |
| [B] joule/second |
| [C] meter/second |
| [D] joule-second |
Answer:
[joule-second]
The dimension of angular momentum is
| [A] [ML2T−1] |
| [B] [ML1T−1] |
| [C] [MLT−1] |
| [D] [ML−2T−1] |
Answer:
[ML2T−1]