When a force is applied to an object, linear acceleration is created. Similarly, applying torque to an object causes angular acceleration of the object. Thus, the role of the force in the case of linear motion is similar to the role of torque in the case of rotational motion. That is, torque is a replica of the force in rotation.
Definition of Moment of Inertia: The ratio of the torque acting on an object relative to an axis of rotation and the resulting angular acceleration of that object is called the inertia of the body relative to that axis of rotation.
Table of contents
- Physical Significance of Moment of Inertia:
- Unit & Dimension of Moment of Inertia:
- Relation: Moment of Inertia Torque and Angular Acceleration:
- Important Information Regarding Moment of Inertia:
- Moment of Inertia: A Scalar or Vector?
- Moment of Inertia for some Uniform Body:
- Radius of Gyration
- Moment of Inertia: Exercise Solution
- Moment of Inertia: Question Answers
Physical Significance of Moment of Inertia:
As mentioned earlier, the role of mass in linear motion is similar to that of inertia in rotational motion. The reason for saying this is clearly from the discussion below.
We know that in the case of linear motion, the mass of an object can be called its translational inertia. This is because the mass of an object is its cause, which prevents it from changing its linear motion. In the case of rotational motion, an object is forced to change its position only when torque (which is a replica of the force in rotation) is applied to the object from the outside; When torque is not applied, the object either stays stationary or the object continues to rotate at equal angular velocity. That is, the inertia of an object in the case of rotational motion can be called its rotational inertia. Because (about to a certain axis) the amount of obstruction that an object has to change the speed of rotation of an object is its (about to that axis) inertia. In short, the relation of inertia to the force and the relation of the moment of inertia to the torque are equivalent.
Obviously, the greater the inertia of an object relative to an axis, the more torque must be applied to rotate the object or to stop the rotation of the object about that axis.
Unit & Dimension of Moment of Inertia:
We know, the moment of inertia is I = mr2,
Unit of Moment of inertia = unit of mass × unit of (distance)2
Unit of Moment of Inertia = Kg × m2
Dimension: = [ML2]
| SI unit of Moment of Inertia | Kg ⋅ m2 |
| CGS unit of Moment of Inertia | g ⋅ cm2 |
| FPS unit of Moment of Inertia | Ib ⋅ ft2 |
Read More: Measurement of Physical Quantity and Unit: Notes
Relation: Moment of Inertia Torque and Angular Acceleration:
The Relation: τ = Iα
Proof of τ = Iα
Suppose a body PQR is rotating around the axis AB with angular acceleration α [Figure 1]. The total mass of the body can be considered as a sum of a large number of particles of masses m1, m2. m3, …. The distances of the particles from the rotation axis AB are r1, r2, r3, … .etc. respectively. For pure rotation, the axis AB remains fixed, as a result, the angular acceleration of each particle remains the same. But the distances of particles from the fixed axis AB are not the same. So, their linear accelerations are different.

Now, if the linear acceleration of particle of mass m1 is a1, then a1 = r1α.
Thus the applied force on the particle 1 is F1 = m1a1 = m1r1α.
Similarly, the applied force on the particle 2 is F2 = m2a2 = m2r2α. and so on for other particles.
Now the moment of force F1 about the axis, = τ1 then,
τ1 = Force distance of the × particle from the axis
τ1 = F1 × r1 = m1r12α
Similarly, for particle 2, τ2 = F2 × r2 = m2r22α
In this way, we can calculate the moment of force for all the particles. So, the total moment of force or Torque of the entire body is the sum individual torque of all the particles. That is the total torque
τ =τ1 + τ2 + τ3 + ….
or, τ = m1r12α + m2r22α + m3r32α + ….
or, τ = (m1r12 + m2r22 + m3r32 + ….) × α
Where I = moment of inertia
For continuous body, the moment of inertia
Where dm = infinitesimally small mass.
Torque = Moment of Inertia × Angular Acceleration τ = Iα
This is the relation between torque and angular acceleration with the moment of inertia. Here should be noted that the torque is an axial vector whose direction is along the direction of angular acceleration.
Important Information Regarding Moment of Inertia:
- The moment of inertia does not depend only on the mass of a body but also depends on the distances of the particles from the axis of rotation, i.e, the distribution of mass.
- For linear motion F = ma; and for rotational motion, τ = Iα. Fo, τ = Iα is the replica of F = ma. Analyzing this we also can say that in linear motion the mass is the counterpart of the moment of inertia in rotational motion.
- In linear motion, what kind of role is played by mass, in rotational motion, the moment of inertia plays the same role.
Moment of Inertia: A Scalar or Vector?
This is a tricky question for students in school or high school. At first, we will answer it for the students of classes 9, 10, 11, or 12. The moment of inertia is a scalar quantity, so here, the answer is yes – it is a scalar. If you look at the formula, you will notice that the terms are mass and square of the distance. Mass is a scalar quantity, as is distance, and the square itself has no direction. As a result, the moment of inertia is a scalar quantity.
Now, for higher-order thinkers, the moment of inertia is neither scalar nor a vector (midway between scalar and vector)- it is a Tensor quantity or more accurately the Moment of Inertia Tensor. It has both magnitude and direction (act both as scalar and vector), but it does not follow the rule of vector algebra.
Note!! Tensor is a multidimensional matrix. A scalar quantity is a tensor of rank 0. Vector quantities are tensor or rank 1. Moment of Inertia is a tensor of higher rank (rank 2).
Moment of Inertia for some Uniform Body:
- For a long rod of length l and mass m: The moment of inertia about the axis passes through the midpoint of the rod is I = (1/12)ml2.
- For a circular disc of radius r and mass m: The moment of inertia about the axis (perpendicular to the plane) passes through the center is I = (1/2)mr2.
- Circular Ring of radius r and mass m, the moment of inertia about the axis passes through the center and perpendicular to the plane is I = mr2.
- For a Solid Sphere of radius r and mass about the diameter, I = (2/5)mr2.
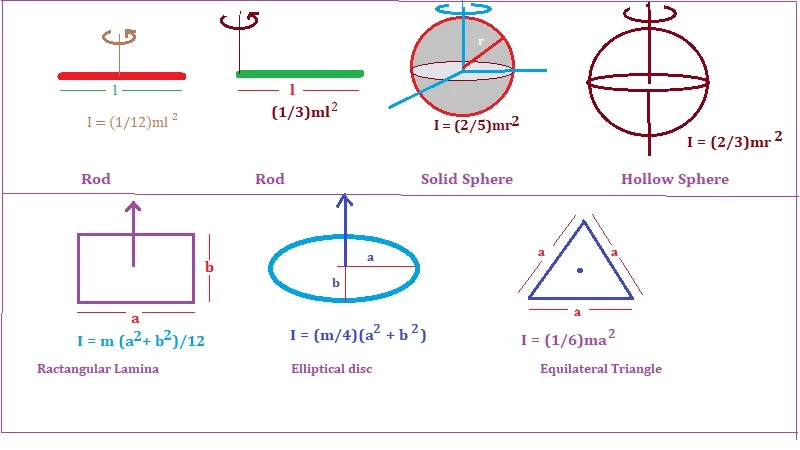
Radius of Gyration
We know that I = Σmr2: = Mk2 (say), where M denotes the mass of the whole body and k is the dimension of length and is called the radius of gyration of the body about the axis. If we consider the whole mass of the body to be concentrated at a single point such that the moment of inertia of this concentrated point mass is same as the moment of inertia of the whole body about the axis, the distance of that single point from the axis is called the radius of gyration of the body about the axis. it is sometimes called the ‘Swing radius‘.
Moment of Inertia: Exercise Solution
Exercise-1: A uniform rod 2 m long weighting 5 kg, is revolving 60 times a minute about one end. Calculate its moment of inertia.
We know, I = Ml2/3, M = 5 kg, l = 2 m.
Therefore, I = (5 × 4)/3 = 6.66 kg-m2.
Exercise-2: Calculate the moment of inertia for a thin circular ring of mass 250 gns and radius 15 cm about an axis in the plane of the ring – when the axis passes through the center in the plane of the circle.
Moment of inertia of the ring about an axis passing through the center and in the plane of the circle, i.e., the moment of inertia of the ring about its diameter = ma2/2, where m = mass of the ring and a = radius of the ring.
The moment of inertia about the diameter = ma2/2 = (250 × 152)/2 = 125 × 125 = 28125 gm.cm2.
Moment of Inertia: Question Answers
Suggested Readings:
Moment of Inertia: Study Notes
