What is Torque?
Torque refers to the twisting force that is responsible for rotation of an object about an axis. The axis may be the center of mass or a fixed point. In another way, we can say that the force that can cause an object to twist about an axis is measured as torque. it is also referred to as the turning effect.
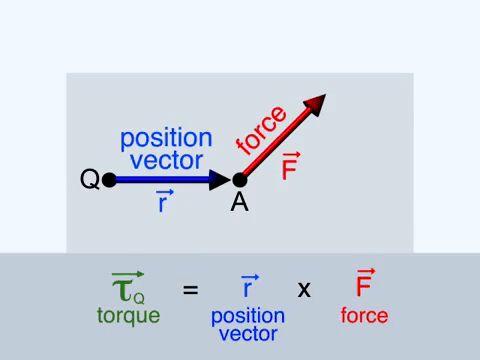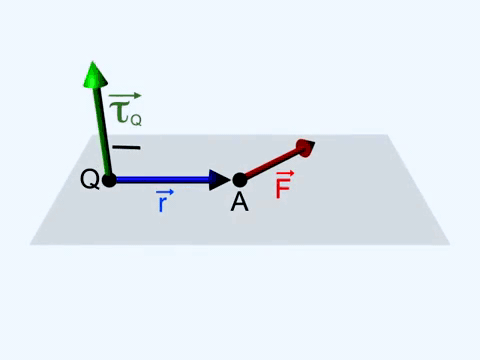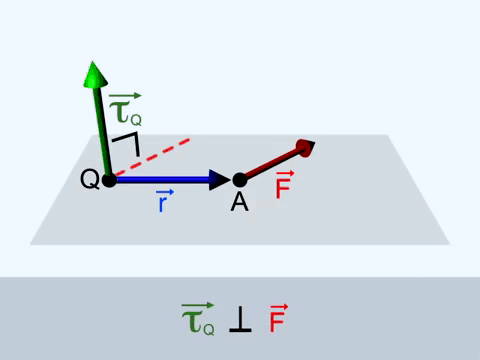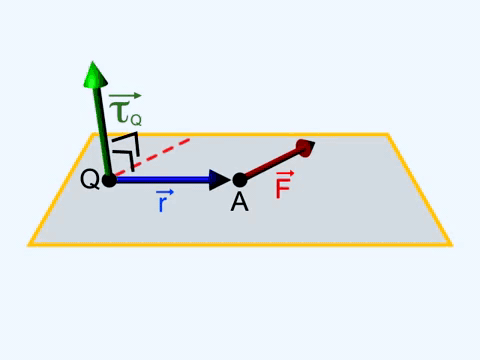
In addition, A force refers to the tendency of an object to rotate around an axis, a fixed point, or a pivot. It is also notified that when two equal and opposite forces act on a body at different points torque is created (actually this is called a couple of forces – we will discuss this later in this article. The visualization figure is attached below.

When torque is applied to a body, it rotates or turns about a certain point or axis. When the body rotates, its angle changes; Therefore, torque forces an object to rotate by changing its angular displacement.
Example: If you want to open a nut or bolt attached to a machine using a wrench, you have to hold the wrench in it and rotate it to generate torque in the handle of the wrench.
Mathematically torque is the vector product of the force acting on an object rotating relative to an axis and the distance of that object from the axis.
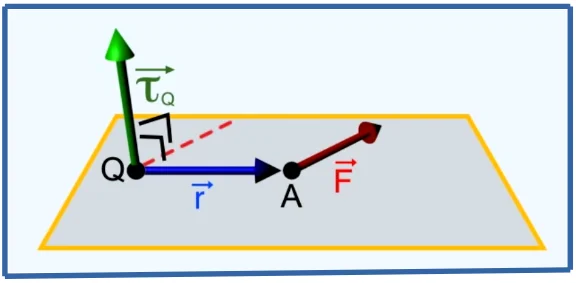
$$\overrightarrow{\tau }=\overrightarrow{r}\times \overrightarrow{F}$$
How to calculate the magnitude of Torque?
The product of the moment force and the moment arm has measured the magnitude of torque. The formula of torque is –
τ = F⋅ r ⋅ sin(θ)
- r = the length of the moment arm
- θ = angle between the force vector and the moment arm.
Now if the angle θ = 90°, Sin(90°) = 1; then,
τ = F⋅ r
Torque – A vector quantity:
Obviously, the torque is a vector quantity. It has both magnitude and direction. The direction of torque can be found using the right-hand thumb rule. When a right-handed skew is rotated anticlockwise, it moves upward when we see it from the top. This upward direction is the direction of torque. For anticlockwise rotation, that is if the force acts along the x-axis and the radius vector is directed towards the y-axis, then the direction of the torque is along the z-axis.
Unit & Dimension of Torque:
Torque = Force × Perpendicular Distance
Unit of Torque = Newton × meter.
The dimension of torque = dimension of force × dimension of displacement.
The dimension of torque [MLT−2]×[L] = [ML2T−2]
| SI unit of Torque | N-m |
| CGS unit of Torque | dyne-cm |
| FPS unit of Torque | poundal-ft |
| Dimension of Torque | [ML2T−2 ] |
Torque produces Pure Rotation:
Torque can only produce pure rotation. As shown in Figure 1, two forces are applied at points A and B, and the magnitude of the total force is F − F = 0. So the object has no linear displacement. But the rotation of the object is caused due to the separation of the action lines of the applied two forces. Therefore, this rotation produces by torque is a pure rotation.
Importance of Torque in Physics:
Torque is a fundamental physics concept that helps us understand how things work in our environment.
- Torque can be used to determine the direction and magnitude of a rotating force applied to an item. It also allows someone to evaluate the possible outcomes.
- In general, torque can be used to detect whether a force is exerted in a counterclockwise or clockwise direction.
- It can also help us determine the angular acceleration with which the object is twisted.
Torque Vs Force:
| Torque | Force |
|---|---|
| The term torque is used in rotational kinematics | The term force is used in linear or translatory motion. |
| Torque = moment of inertia(I) × angular acceleration(α) τ=Iα | Force = mass × acceleration F = ma |
| Work done = torque × angular displacement W= τθ | Work done = Force × displacement(s) W = Fs |
| Power = torque × angular velocity P = τω | Power = force × velocity P = Fv |
Torque and Moment of Force: – Are they the same?
Well! this question is tricky. The torque and the moment of force have the same unit and the same dimension. Also, they are both vector quantities. That’s why they both refer to the same physical quantity. However, in some cases, we can find some minor differences by studying the object’s reaction.
- Torque can rotate a body in a pivot when applied to it. But the moment may not rotate that body, it may deform or bend that body.
- Torque can change the angular momentum of an object. However, the moment does not produce a change in angular momentum.
- Torque is a dynamic force in nature whereas moment is a static force in nature.
- The torque is used to measure the coupling effect. Mont is not associated with coupling.
- Torque is independent of the reference of point while the moment of force is defined with respect to a definite point of reference.
Relation between Torque and Moment of force:
In the above paragraph, we have discussed the torque and moment of force. Here, we are going to establish the relationship between these two quantities.
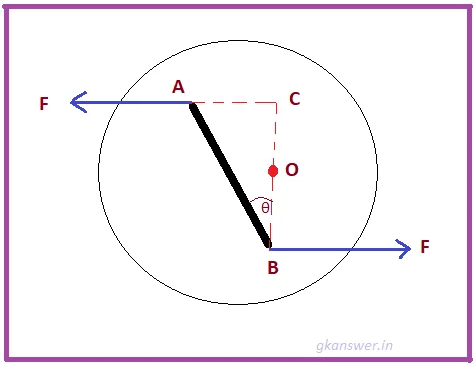
Let us consider the above figure -4.
The moment of force F about the point O = F × CO
Also, the moment of force F about point O is F × BO.
So the total algebraic sum of the moment of these two forces is = P × CO + P × BO
= P × (CO + BO) = P × BC
Now, P × BC is the torque of two forces F.
Thus, The torque about the point O = Moments of two forces about the point O.
Couple:
A couple is a set of forces that are of equal magnitude, exerted in opposite directions, and separated by a perpendicular distance
Application of Torque and Couple:
- To open/close any door.
- A person driving a car using the steering wheel
- Turn left or right on the bicycle.
- Twisting a bottle lid to open or close.
- The wringing of clothes by hand. And many more…
Work done by Couple/Torque:
We know that the couple is a combination of two forces. When a couple creates rotation of an object then the work done by two equal forces (moment) is the total work done by the torque. Now torque, by definition:
τ = F × AB.

Now let us consider that the object rotates at an angle θ by the application of couple. As a result, point A displaced to A1 and point B to B1. If θ is small then the arc AA1 and BB1 can be considered as a straight line (that’s why I’ve used the word “displace” in the previous line).
Now AA1 = AO × θ and BB1 = BO × θ
The work done at point A due to force F = W1 = F × AA1 = F × AO × θ
Similarly, work done at point B due to force F =W2 = F × BB1 = F × BO × θ
Therefore the total work done by the couple is W = W1 + W2
or, W = F × AO × θ + F × BO × θ
or, W = F • (AO • θ + BO • θ)
or, W = F × (AB) × θ [since AB = AO + BO]
or, W = τ × θ [τ = F × AB]
Work done = torque × angular displacement.
Note: Here we can see that the work done is not dependent on the axis of rotation.
For one complete rotation, the angular displacement is 2π. So, for n number of complete rotations, the total displacement is 2nπ. For n rotation, the total work done is W = 2nπ × τ.
How does torque Relate to Energy and Power?
One of the most confusing things about torque and energy is that they both have the same dimensions and units (N.m). However, both things are quite different – they measure different things. Their relationship can be derived as follows:
We know that the Power P = Force × Velocity
or, P = F × distance /time
For one complete rotation the distance = 2πr
Where r = radius of the circular path.
So, P = F × 2πr / t
or, P = (F × r) 2π/t
We know that torque τ = F × r
and angular velocity ω = 2π/t
Therefore, Power P = τ × ω.
Thus in rotational kinematics, the rotation power P = torque angular × velocity. This is equivalent to the formula Power P = force × velocity in linear kinematics.
Note: The (Newton-meter) and (Joules) units are dimensionally identical, but torque and energy are not the same. The difference is that in the unit of torque, there are also radians, which we treat as dimensionless. Radian is still in the expression for torque but not in the expression of energy.
How can we enhance/reduce torque?
We know that by increasing or decreasing the length of the lever, we can increase or decrease the effect of force on an object. Similarly in rotational motion, the torque can be increased or decreased by using gear. A proportional drop in rotational speed is associated with an increase in torque.
We can see that a bicycle, car, motor, and other engines use gears of different diameters. Using the suitable diameter of the gear, the performance can be increased or decreased.
Torque: Problem Solution
Exercise-1: Two objects of mass 2 kg and 5 kg are hung on either side of a 1.4 m long light bar. At what point of the bar will the equivalent point?

Answer:
If the bar remains horizontal, it has no rotational motion. Let us consider that point O is the equilibrium position. From the figure, we can see that the rotation of the bar due to 2 kg is anticlockwise and for 5 kg it is clockwise. So the moment due to 2 kg is positive and due to 5 kg is negative.
The moment of force due to 2 kg is = + 2 × OA. (about point O)
The moment of force due to 5 kg is = − 5 × OB. (about point O)
So, the bar remains in equilibrium if the total moment of force is zero with respect to point O.
Total moment = 2 × OA − 5 × OB = 0
or, 2 × x − 5 × (1.4 − x) = 0
or, 7x = 7
or, x =1
Thus the equilibrium point is at a distance of 1 m from the end A i.e. the end has a mass of 2 kg.
Exercise-2: Let us consider an L-shaped bar ABC. At point B, the two arms (AB = 20 cm BC = 30 cm) of the bar make 90°. The whole bar is hung at point B as shown in the figure below. How much angle does the arm BC makes with the vertical line drawn through point B?

Answer:
According to the figure, the arm BC makes an angle θ with the vertical line through point B. Also consider the mass per unit length is w.
The mass of AB = 20w
The mass of BC = 30w.
At equilibrium, the total moment about O is = 0.
So 20 wx = 30 wx
or, 20 × 10Cosθ = 30 × 15Cosθ
[since the average mass is the mass of the half of each arm(20/2 = 10 and 30/2 = 15)]
or, tanθ = 4/5
or, θ = 24°
FAQ on Torque:
Few MCQs on Torque
What is torque in the context of physics and mechanics?
[The rotational equivalent of force that causes rotational motion.]
Which of the following factors does torque depend on?
[C] Length of the lever arm.
If you want to increase the torque produced by a force on a lever, which of the following should you do?
[A] Increase the force applied.
Which of the following statements about torque and rotational equilibrium is true?
[A] Torque is zero when an object is in rotational equilibrium.
In which unit is torque typically measured?
[D] Newton-meters (Nm).
Torque: Practice Problems
Two objects with the same mass are attached to a rotating platform. Object A is located closer to the center of the platform, while Object B is located farther from the center. Which object experiences a greater torque when the platform is rotated with the same force?
A door is hinged on one side and can rotate freely. Where should you apply a force on the door to make it easier to open?
A wrench is used to tighten a nut by applying a force of 50 N at the end of a 0.2-meter-long wrench. What is the torque applied to the nut?
A force of 20 N is applied at an angle of 30 degrees to a wrench. What is the effective torque produced by the force?
Torque: Study Notes
Suggested Readings:
