Definition: The force applied to an object and the perpendicular distance of the force from its axis of rotation – the combination of these two factors causes the rotational tendency in the object, is called the Moment of force.
Suppose the handle (AB) of a typical pump is fitted over a tube well [Figure 1]. O is the support point that is fixed. The handle is usually held up and down by the OA portion of the handle. That is, the handle can rotate (on the surface of the page) around the fixed point O. Apparently in this case the axis of rotation lies on point O and is perpendicular to the page of the book. When the OA portion is moved down, the OB portion rises up and the water rises through a piston attached to point B.
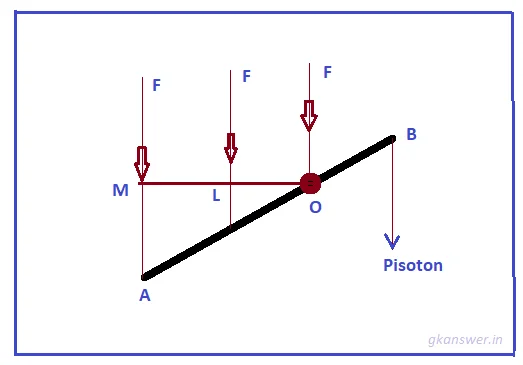
We know from our general experience that the applying force F cannot rotate the handle when applied to the point O. The force F applied a little away from O can rotate the handle but it is difficult to draw water. Practically we feel that.
So it is not always possible to say that an object will rotate only when a force is applied to it. The line of action of a force (OA) is actually responsible to rotate an object only if it is slightly away from the axis of rotation (O). The applied force cannot rotate the object when the action line of the force passes through the center of rotation or the axis of rotation (O). The greater the perpendicular distance of the force from the center of rotation (point O), the greater the rotational tendency of the object, i.e., the easier it is to rotate the object.
The vertical distance of the action line of the applied force from the center of rotation is called the arm of that force. In the given figure, the length of the arms for different operations of force F are 0, OL, and OM. It turns out that the tendency of rotation of an object depends on two factors:
- (i) the magnitude of the applied force (F) and
- (ii) the arm of the applied force (d).
The combination of these two gives rise the rotation.
The product of the magnitude of the applied force and the perpendicular distance of the action of the force from the rotation point gives us the magnitude of the moment of force.
That is moment of force G = force F × perpendicular distance (d).
or G = Fd
In the given figure, the moment of force for the various operations of force F are 0, F×OL, and F×OM. Since OM> OL> O, it can be said that when the length of action of F passes through point A, the magnitude of the moment of force is greater relative to point O.
This means that the handle rotates most easily when the force F is applied to point A (the farthest point). On the other hand, when the force F is applied to the point (O, the closest point) the moment of force is zero, and that force F cannot cause any rotation.
Remember, the presence of the axis of rotation is inevitable in the case of rotation. So to say that the moment of force is relative to a point means it’s subject to an axis of rotation; This axis of rotation is perpendicular to the plane on which the point is located and the force is acting.
Example: In the case of hinged doors, the door opens as easily as it is pushed away from the hinge, but the door does not open as easily when pushed somewhere near the hinge — we all have this experience.
The moment of force is also an axial vector, such as angular displacement, angular velocity, and angular acceleration.
Units and dimensions of Moment of Force:
By definition, the moment of force = the magnitude of the force × Perpendicular distance from the axis of rotation to the point of application of the force.
So, the unit moment of force = unit of force × unit of distance.
| CGS unit of moment of force | dyne-cm |
| SI unit of moment of force | Newton-meter |
| FPS unit of moment of force | poundal -ft |
The dimension of a moment of force = dimension of force × dimension of distance
The dimension of moment of force = [MLT−2] × [L] = [ML2T−2]
Algebraic Sign of Moment of Force:
We know that when multiple forces operate on the same plane, they are called coplanar forces. In the application of more than one force, the rotation of an object is limited to the plane of those forces. Suppose that an object AB with respect to the point O can rotate in a certain plane (such as the surface of a page) (Figure 2).
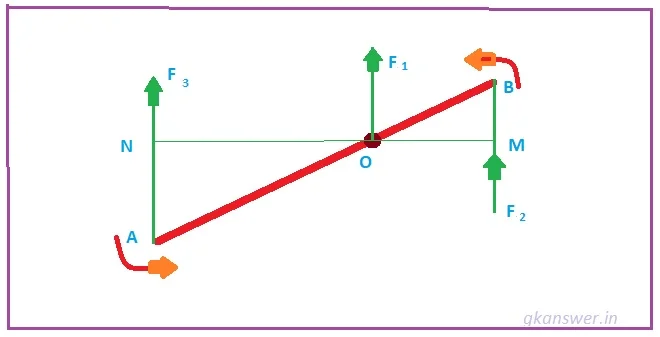
By careful observation of the figure, we can understand that
- The moment of force of F1 = zero.
- The moment of force of F2 is anticlockwise because it can create anticlockwise rotation. That’s why for anticlockwise rotation the moment is POSITIVE.
- The moment of force F3 is anticlockwise and creates a clockwise rotation. So, for clockwise rotation the moment of force is NEGATIVE.
Thus it is found that the moment of force can be expressed by a simple algebraic sum and the magnitude of this sum can be positive or negative.
Algebraic Sum of Moment of Force:
Let us consider three coplanar forces F1, F2, and F3 acting on points O, B, and A of an object AB respectively (fig-2). The total algebraic sum or resultant moment of force (G) is, –
G = F1 × 0 + F2 × OM + F3 × ON
- Now if G = 0, then no rotation occurs.
- If G = Positive, then the rotation is anticlockwise.
- And, if G = Negative, then the rotation is clockwise.
Moment of force: Vector Formula
The cross products of the r vector and the force vector F will equal the moment vector G around point O.
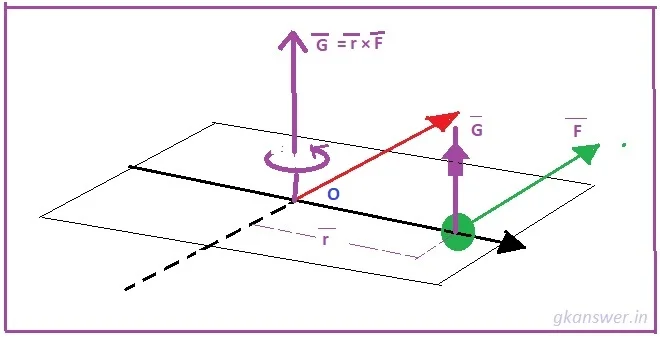
The moment of Force is a vector quantity. From the above figure, one could imagine the direction moment. The direction follows the vector cross product rule or right-hand rule. The vector form of the moment is given below.
Exercise-1: Find the moment of force F = 6i − 3j, applied at (4, 5) about the point (1, 2).
Here in this problem, a force F = 6i − 3j is acting on point B (4,5). We have to find out the moment of this force about point A (1,2).
The formula of the moment of force (G) is given by –
Here,
And,
From the Triangle Law of Vector Addition, we can easily find the r vector.
Therefore, the magnitude of the moment of the force is − 27. As it is negative, the direction will be clockwise.
Suggested Readings:
Moment of Force: Study Notes
