Kinetic energy can be found in every moving material. We know how to calculate this for a body moving in one direction, but what about a rigid body rotating i.e. continuously changing its direction? Because each point on the rigid body has a different linear velocity, this may appear difficult. However, we can represent the kinetic energy of a rotating object using angular velocity (ω), which is the same for a completely rigid body.
The product of the moment of inertia and the square of the angular velocity is called rotational kinetic energy. Therefore by this definition, the rotational kinetic energy can be expressed in terms of the moment of inertia (I) and angular velocity (ω). The rotational K.E of an object is analogous to linear kinetic energy.
Formula of Rotational Kinetic Energy:
The formula for the rotational kinetic energy of an object is given by –
Where Erotational = Rotational Kinetic Energy
I = Moment of Inertia
ω = Angular Velocity.
Derivation of Rotational Kinetic Energy:
Let us consider a body PQR rotating about an axis AB with angular velocity ω [figure-1]. Due to this rotation, the body has some kinetic energy, which is rotational KE. Now the body can be considered as a sum of a large number of particles having masses m1, m2, m3, …. etc. These particles are located at distances r1, r2, r3, … etc. with respect to the axis of rotation AB. As the body is rigid, the angular velocities of all the particles remain the same i.e, angular velocity ω = constant. But the linear velocities (v) of all particles are not the same since the distances of the particles are different from the axis AB.
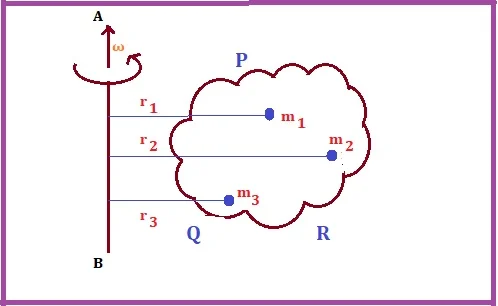
Now,
Particle of mass m1 has velocity v1. Thus, v1 = ωr1
Particle of mass m2 has velocity v2. Thus, v2 = ωr2
Particle of mass m3 has velocity v3. Thus, v3 = ωr3
The Kinetic Energy of particle 1 is = (1/2)m1v12 = (1/2)m1ω2r12
The Kinetic Energy of particle 2 is = (1/2)m2v22 = (1/2)m2ω2r22
The Kinetic Energy of particle 3 is = (1/2)m3v32 = (1/2)m3ω2r32
…. and so on ….
Therefore, by summing up all the kinetic energies of the particles, we get the total Kinetic energy.
Total rotational kinetic energy = [(1/2)m1ωr12 + (1/2)m2ωr22 + (1/2)m3ωr32 + …. ]
= (1/2)ω[m1r12 + m2r22 + m3r32 + …. ]
= (1/2)ω2 Σmr2
= (1/2)Iω2
Where I = Σmr2 = Moment of Inertia about the axis.
Therefore, the rotational kinetic energy = Iω2/2
In translational motion the translational kinetic energy = (1/2)mv2.
Unit and Dimension of Rotation K.E
The unit and dimension of rotational kinetic energy are given in the table below.
| SI unit of Rotational K.E | Joules (J) |
| MKS unit of Rotational K.E | kg.m2.s−2 |
| CGS unit of Rotational K.E | g.cm2.s−2 |
| Dimension of Rotational K.E | [M L2 T-2] |
Derivation of SI Unit of Rotational K.E
Rotational Kinetic Energy = Iω2/2
Unit of Rotational K.E = [unit of Moment of Inertia] × [unit of Angular velocity]2
= [Kg ⋅ m2] × [s –1]2
= [Kg ⋅ m2s –2] = [Kg ⋅ m ⋅ s –2] × [m]
= [unit of force] × [unit of displacement]
= [unit of word done]
= [unit of energy]
= Joule
Derivation of Dimension of Rotational K.E
We know that, Rotational Kinetic Energy = (1/2) × [Moment of Inertia] × [Angular velocity]2
Dimension of Rotational K.E = [Dimension of Moment of Inertia] × [Dimension of Angular velocity]2
Dimension of rotational K.E = [ML2] × [T –1]2
= [ML2T –2]
Thus, the dimension of rotational kinetic energy is = [ML2T –2]
Rotational Power:
If an object rotates with angular velocity ω by the application of torque τ, then
Rotational Power = (work done)/time
= (torque × angular displacement) / time
= torque × angular velocity
= τω
Rotational Power P = τω
Rotational KE: Problem Solution
Exercise-1: A disk is rotating with an angular velocity of 10 rad/s. its moment of inertia is 5 kg.m2.
Answer: We know the rotational kinetic energy Erot = (1/2)Iω2.
Here in this problem, we have a moment of inertia I = 5 kg.m2 and angular velocity ω = 10 rad/s
to Erot = (1/2) × 5 × 102 = 250 Joule
Exercise-2: A wheel is rotating with rotational KE 2500 J. If its angular velocity is 5 rad/s, then what is the moment of inertia?
Answer: Here, Erot = 2500 J, and ω = 5 rad/s. So by using formula Erot = (1/2)Iω2, we get:
Moment of Inertia I = 2 × Erot /ω2
= 2 × 2500 /52
= 5000/25
= 200 kg.m2
Exercise-3: An rotating object has rotational KE 600 erg. Its moment of inertia is 50 kg.m2. What is its angular velocity?
Answer: Here rotational KE Erot = 600 J. Moment of inertia = 50 kg.m2.
So Erot = (1/2)Iω2
or, ω2 = 2 Erot /I
or ω2 = 2 × 600 / 50
or ω2 = 1200/50 = 24
or ω = √(24) ≈ 4.898 rad/s
Therefore, the angular velocity of the particle is 4.898 rad/s
Rotational KE: Question Answers
Suggested Readings:
Rotational Kinetic Energy: Study Notes
