Centripetal force:
Definition:
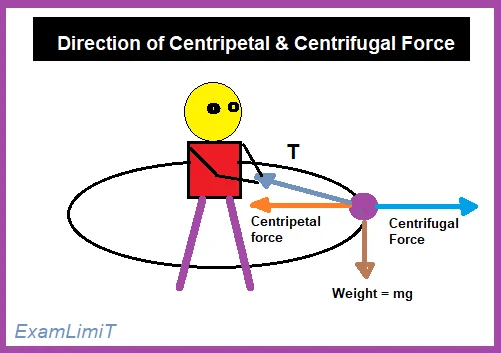
A force that acts perpendicular to the linear velocity of an object to rotate it in a circular path and acts towards the center of that circular path is called a centrifugal force.
Concept/Explanation of Centripetal force:
According to Newton’s first law of motion, if no force is applied to an object from outside, the object remains stationary or moves at the same speed, that is, the object cannot move in a circular path. Thus, in order to rotate the object in a circular path, an external force must act on the object. Also, we know that the acceleration of a rotating object is always centripetal i.e it is always directed toward the center or axis of rotation. Then, the force acting on a rotating object would also be centripetal. This force acts towards the center (or axis of rotation) along the radius (or line joining between the axis and the object). This external force is known as the centripetal force. So we can say that it is the centripetal force that causes an object to move in a circular path by deviating from the state of motion at the same linear speed.
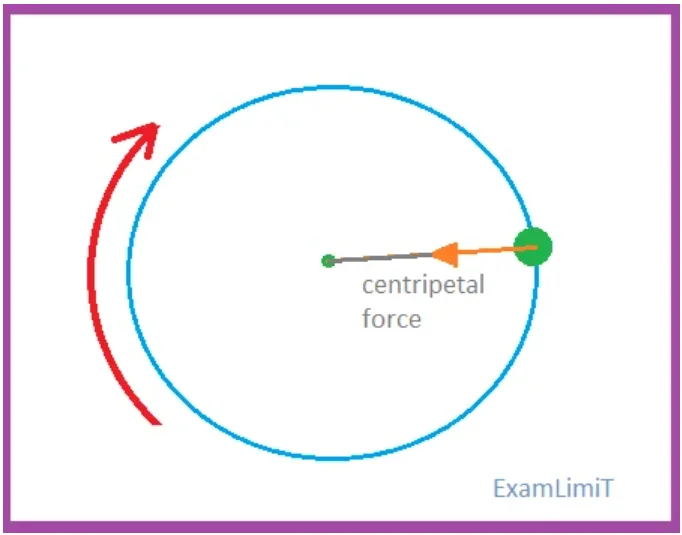
The formula of Centripetal Force:
As we have seen in the preceding chapter, the formula of centripetal acceleration in a uniform circular motion is ωr. Thus, if m is the mass of an object, then according to Newton’s second law,
Force = Mass × Acceleration
or F = m × ωr = mv2/r
Therefore the formula of centripetal force is –
- Where, Fc = Centripetal Force,
- m = mass of an object
- r = radius of the circular path,
- v = linear velocity
- ω = Angular Velocity.
Note 1: It may be mentioned that the centripetal force is called the no-work force. This force does not do any kind of work because there is no displacement of the object along the direction of centripetal force.
Note 2: Centripetal force ∝ velocity2. This means if we double the velocity then 4 times of centripetal force is required to keep an object rotating in a circular path.
Unit and Dimension of Centripetal Force:
Unit: Newton (N) in SI system and dyne in CGS system.
Dimensions: [M1 L1 T-2]
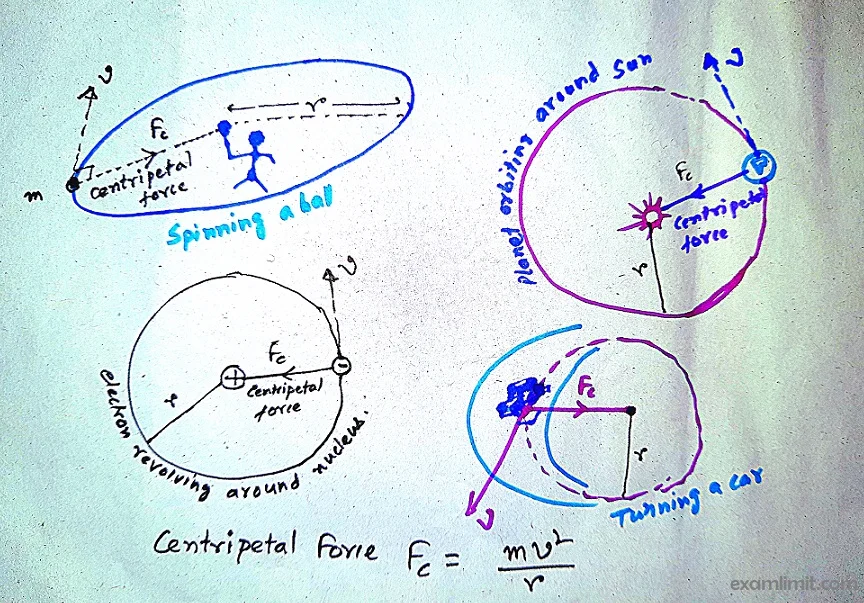
Practical examples of Centripetal force:
- When a stone is tied to a string and rotated in a circle, the string pulls the stone toward the center. That pull or tension of the string is the centripetal force.
- When riding a bicycle in a circular path, the friction between the road and the bicycle’s wheel provides the necessary centripetal force for the bicycle to move in a circular path.
- The Sun’s gravitational pull on any planet provides the required centripetal force to rotate the planet around the Sun.
- Positively charged nucleus and negatively charged electrons within the atom – the mutual electric force of attraction between these two provides the necessary centripetal force to rotate the electrons around the nucleus.
The motion of a Cyclist on a Horizontal Circular Track:
Let us consider a cyclist taking a turn around a curve road (not banked) of radius r and speed v. In that case he makes an angle θ with the vertical axis OB. So the normal force of the cyclist is R tilted at an angle θ with OB. Its verticle component is Rcos θ along OB and the horizontal component is R sin θ along OA.
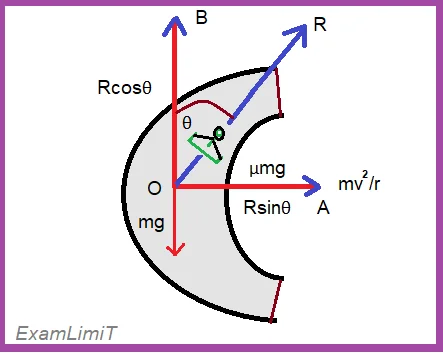
Here 4 types of force are acting on point O.
- Normal force R
- Weight of the cyclist mg
- frictional force μmg between tyre and road.
- centripetal force mv2/r
The verticle component of normal force (Rcos θ ) balances out the weight (mg) of the cyclist. Also, the frictional force provides the necessary centripetal force.
(1) Rcosθ = mg
(2) Rsinθ = mv2/r
Dividing these two equations we get,
(3) tanθ = v2/(rg)
From equation (3) we can see that if the speed of the cyclist is increased and the radius decreases then the value of θ increases. The limiting friction between the road and the tyre of cyclists is μmg. Where μ is the coefficient of friction. This value of the limiting friction is the maximum centripetal force so that the cyclist does not sleep and fall on the road. If vm is the maximum speed (with maximum tilted angle θm) of the cyclist then,
mvm2/r = μmg
vm2 = μrg
vm = √(μrg) —-(4)
And tanθm = vm2/(rg) = μrg/(rg) = μ —(5)
Note that equations (3) (4) and (5) do not depend on the mass of the cyclist.
1. Which provides the centripetal force for the rotation of planets around the sun?
2. Where the weight of an object on the earth is maximum?
3. Why should the maximum speed limit indicator board be installed at the bend of the road or the bend of the railway line?
Centrifugal Force
Definition: The apparent force that an object moving along a curved path experiences as it moves away from the center of rotation is known as centrifugal force.
Centrifugal force is a fictitious force also called inertial force. It is an apparent outward force acting on a rotating object. It is not a real force according to Newton’s laws.
If an object rotates in a circular path with an angular velocity and an observer moves along with the object with the same angular velocity, then the observer perceives that a force equal and opposite to the centripetal force is acting on the rotating object. That force is called centrifugal force.
Formula of Centrifugal force:
To calculate Centripetal Force and centrifugal force both, we may use the same formula. However, centrifugal force is equal and opposite to centripetal force, a negative sign is used here.
Understanding of Centrifugal force:
Let’s say a merry-go-round that can rotate horizontally is in a steady state. A person is sitting in that merry-go-round and has a stone in his hand. This time, the merry-go-round began to rotate at the constant angular velocity. As a result, the stone will also turn around in the circle with the person.
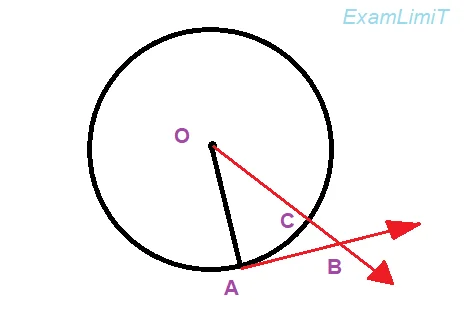
Now, the following two observers will discuss the speed of the stone in two ways.
An observer’s view standing on the ground:
Since the stone is rotating in a circle, this observer will say that a Centripetal Force is acting on the stone. Because we know that only the centripetal force is responsible for an object to rotate in a circle. If the observer sitting in the merry-go-round releases the stone from his hand at point A, the observer from the ground will see the stone running along the tangent of the circle, i.e. along path AB due to the inertia of motion.
An observer’s view sitting on the merry-go-round:
This observer is rotating at the same angular velocity as the stone. So, with respect to him, the stone is in the same position. That is, he will think the stone is fixed at the same position. If this observer releases the stone from his hand at point A, after a while the stone reaches point B, as well as the observer rotating in the merry-go-round will reach point C. So the direction of motion of the stone will be outward from the center, i.e along CB. He would think, the stone is moving outward along the radius of the circle under the influence of a force. This force is centrifugal force.
Note that point B or C here is located very close to point A, ie AB ≈ arc length AC.
Centrifugal Force – a Pseudo force (also known as Fictitious Force):
From the above discussion, we can see that the centrifugal force does not exist with respect to the observer standing on the ground or earth’s surface which is the rest frame of reference or inertial frame of reference. This force exists only with respect to the observer revolving around a circular path which is a non-inertial frame of reference (Accelerated frame). Thus the centrifugal force does not exist in an inertial frame of reference. That’s why centrifugal force is a Pseudo or Fictitious Force.
Practical examples of Centrifugal force:
- Centrifuge: This is basically a vessel rotating at a high angular velocity around an axis. With this device, the suspended particles can be separated from a liquid. With the help of this, butter is collected from the milk. The butter particle is lighter than the milk. While rotating at high speed the butter remains close to the axis of rotation and the skimmed milk moves away.
- A wet cloth drying machine is also a type of centrifuge. With the help, of centrifugal force, the water particles move away through the small hole.
- Loss of weight of a body due to the earth’s diurnal motion.
- Flattening of the earth at the poles due to the centrifugal force.
1. Why do the passengers feel less weight when the vehicle is traveling on a convex road?
2. Why do you feel light at the highest point and heavy at the lowest point when riding a marry go round?
Difference Between Centripetal & Centrifugal force:
| Centripetal force | Centrifugal force |
|---|---|
| Exists in an Inertial frame. | Exist in Non-inertial frame. |
| It is a real force. | It is a Pseudo force. |
| Its direction is toward the center. | Its direction is outward of the center. |
| It is caused due to real forces like tension, gravity, etc. | It is caused due to the inertia of an object. |
FAQ on Centripetal/Centrifugal Force:
/
Exercise solution:
A stone of mass 2kg is attached to a string of radius 2m and rotates 4 times per second. What is the centripetal force acting on the stone?
Answer: Here mass, m = 2kg
radius, r = 2m
Centripetal force is given by the formula Fc = mv2/r
So we need to find the linear velocity (v) of the stone:
Now, the stone rotates 4 times/sec means its frequency is f = 4 /sec.
The length of one complete rotation (λ) is equal to the circumference of the circle:
That is λ = 2πr = 2π × 2 = 4π
Therefore, the linear velocity v = fλ = 4 × 4π = 16π m/s
∴ Centripetal force Fc = [2(16π)2]/2 = 2526.68 N
On a merry-go-round of a 5 m radius, a 50-kilogram boy is rotating with it. If the boy’s velocity is 10 m/s, what is the centripetal force on him?
Answer: Given r = 5 m
mass, m = 50 kg
velocity, v = 10 m/s
Centripetal Force, Fc = mv2/r
∴Fc = 50⋅102/5 = 1000 N
A car traveling at 10 m/s over a hill makes the passengers feel weightless. Obtain the hill’s radius of curvature.
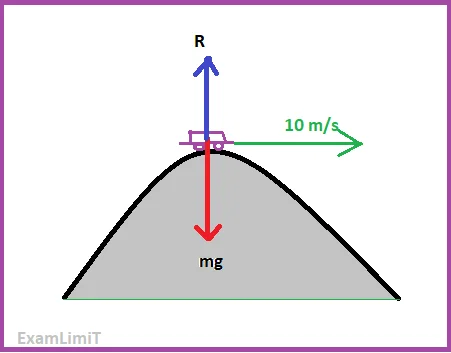
Answer: Let the mass of the car be m. If mg is the weight of the car, then the passengers feel weight R. Therefore:
mg − R = mv2/r
As the passengers feel weightless, so apparent weight R = 0;
mg = mv2/r
⇒ r = v2 /g
⇒ r = 102/9.8 = 10.2 m (approx.)
A cyclist is moving at a speed of 36 km per hour on a circular path of a radius of 30m. How much is its vertical inclination?
Answer: Let the angle of inclination of the cyclist with the vertical = θ
Velocity of the cyclist, v = (36 x 1000) ÷ (60 x 60) = 10 m/s
The radius of the circular path = 30 m.
We have, tanθ = v2/(rg)
⇒ tanθ = (10 × 10) ÷ (30 × 9.8)
⇒ tanθ ≈ 0.34
⇒ θ = tan−1 (0.34)
∴ θ = 18.78°
This is the inclination angle with the verticle axis.
Practice Problems:
A ball of wool is suspended from the roof of a car by means of a light bar of 1 m long. What angle does the bar make with the horizontal path? [IIT ’92] [Answer: 45°]
A small coin is placed 7 cm from the rotating disc of a gramophone. By gradually increasing the rotation rate from zero, the coin starts moving outwards when the rotation rate is 60 times per minute. If the coin is placed 12 cm from the axis, at what rate of rotation will the coin start moving? [Answer 45.8 rpm]
A cyclist tilts at an angle of 30° with respect to the vertical while turning in a circular path at 36 km/h. What is the radius of the path? [Answer: 17.7m]
A cyclist is traveling in a circular path with a velocity of 10 m/s. If the radius of the circular path is 80 m, find the angular velocity of the cyclist. [Answer: (1/8) rad/sec]
Check your knowledge of Centripetal force:
A truck driver suddenly saw a wall some distance ahead of him. To stop the truck he will
[A] immediately applies the brakes
Which of the following is a pseudo-force?
[B] Centrifugal force
The coefficient of friction of the road and wheel is 0.6. At what maximum speed can the car safely traverse a bend of radius 150 m?
[C] 30 m/s
An object of mass 1 kg is tied by a string and placed on a horizontal plane. Keeping the thread horizontal, the object started to rotate in a circular path at an angular velocity of 3 rpm. Now, if the tension of the string is increased by 4 times, what will be the change in velocity of the object?
[] 12 rpm
The radius of a curve road is r and the coefficient of friction between the car and the road is μ. What is the maximum speed at which the car will not skid while turning?
[A] vm = √(μrg)
Suggested Readings
Download: Centripetal Force Centrifugal Force Notes
Download PDF
